Quasi Normal Modes
Resonance is a central phenomenon in physics. In the context of electromagnetism, I study open resonators to predict their spectral properties through the computation of their quasi-normal modes associated with complex eigenfrequencies of Maxwell’s operator.
Open resonators and quasimodal expansion
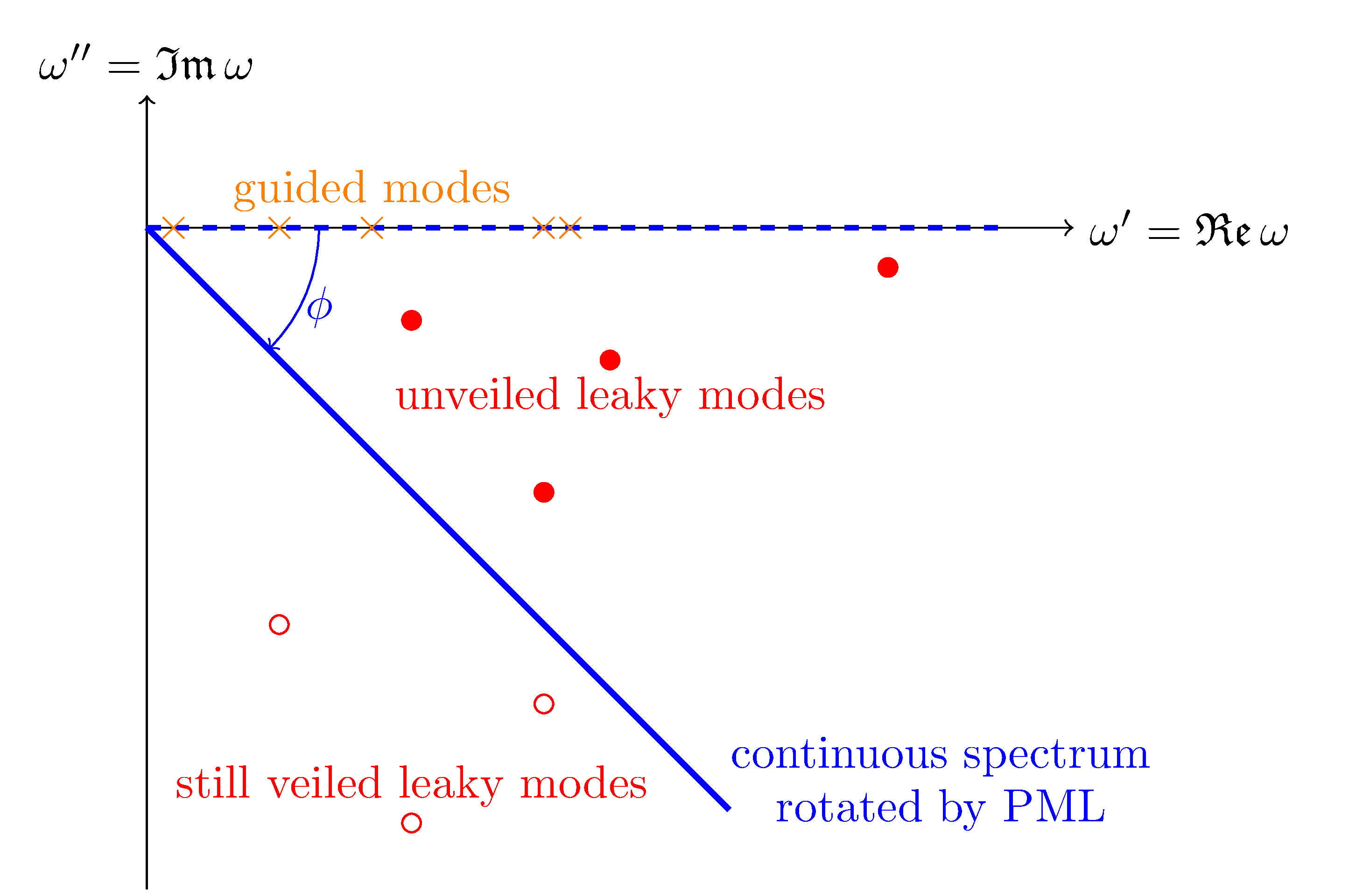
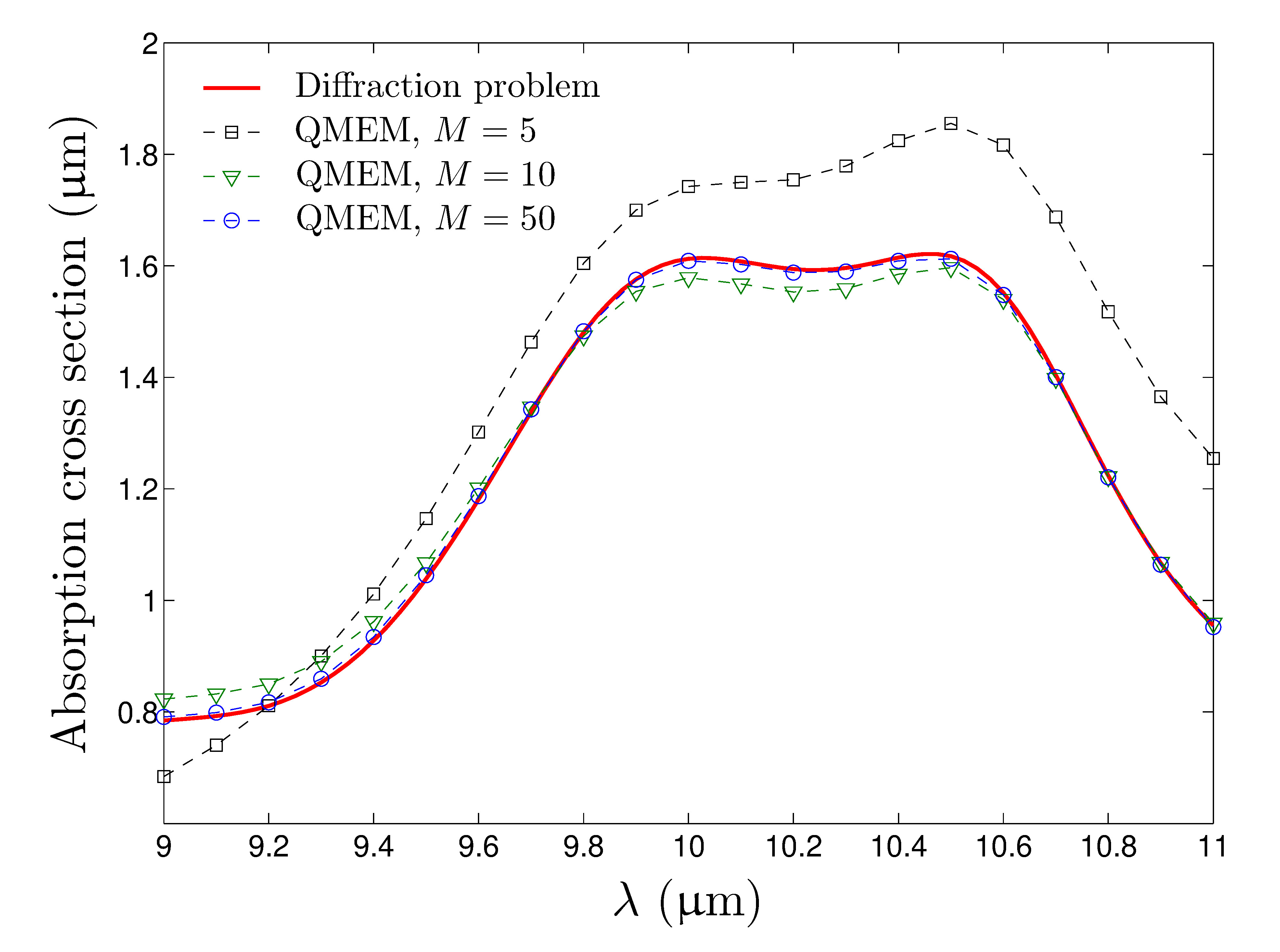
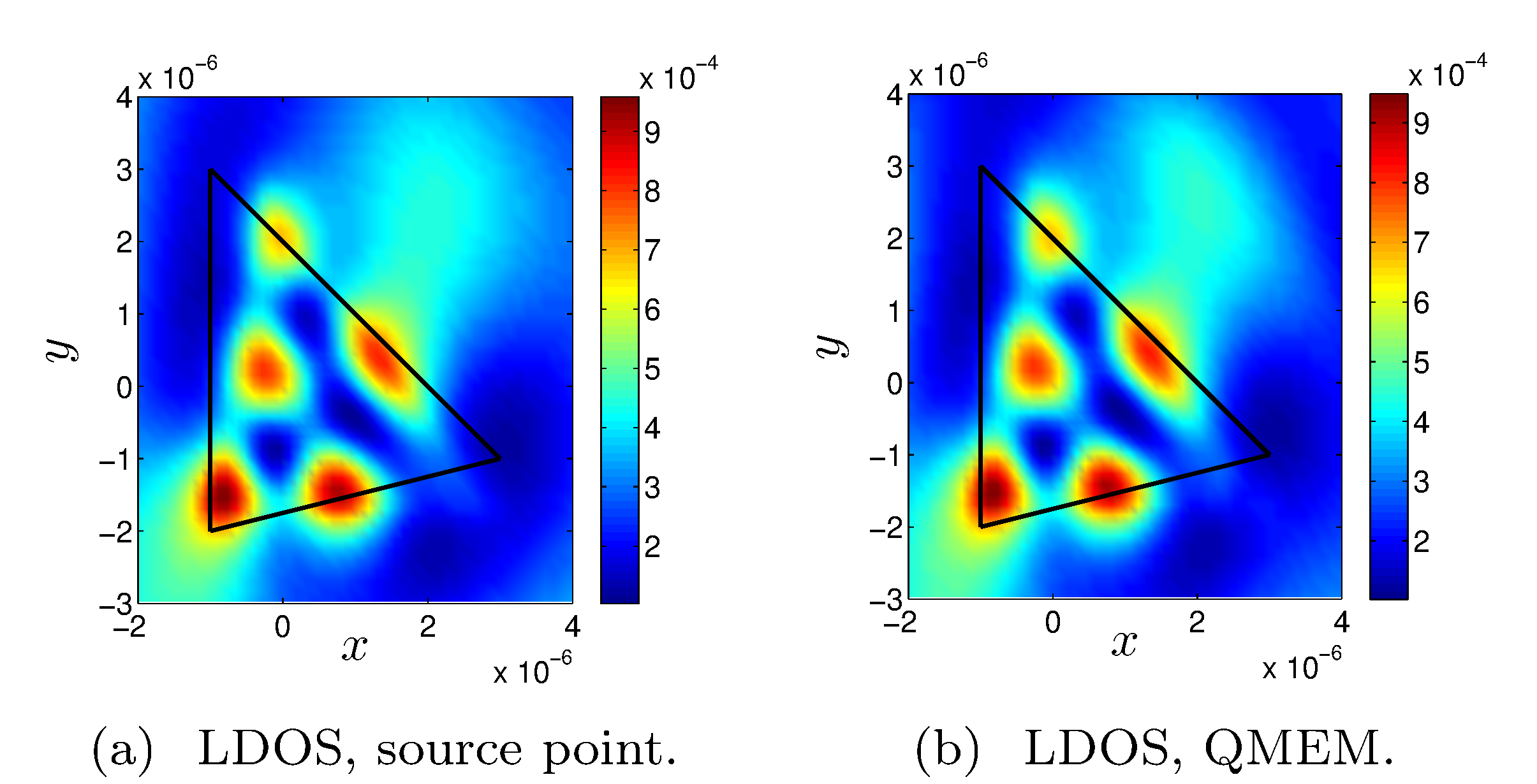
During my PhD, I developed a quasimodal expansion method (QMEM) to model and understand the scattering properties of arbitrary shaped two-dimensional open structures. In contrast with the bounded case which has only a discrete spectrum (real in the lossless media case), open resonators show a continuous spectrum composed of radiation modes and may also be characterized by resonances associated to complex eigenvalues (quasimodes). The use of a complex change of coordinates to build perfectly matched layers allows the numerical computation of those quasimodes and of approximate radiation modes. Unfortunately, the transformed operator at stake is no longer self-adjoint, and classical modal expansion fails. To cope with this issue, we consider an adjoint eigenvalue problem whose eigenvectors are biorthogonal to the eigenvectors of the initial problem. The scattered field is expanded on this complete set of modes leading to a reduced order model of the initial problem. The different contributions of the eigenmodes to the scattered field unambiguously appears through the modal coefficients, allowing us to analyze how a given mode is excited when changing incidence parameters. This gives physical insights to the spectral properties of different open structures such as nanoparticles and diffraction gratings. Moreover, the QMEM proves to be extremely efficient for the computation of local density of states.
Related article
- B. Vial, F. Zolla, A. Nicolet, and M. Commandré, Quasimodal expansion of electromagnetic fields in open two-dimensional structures. Phys. Rev. A 89 (2):023829, (2014) DOI | URL
Coupling model and mode hybridization
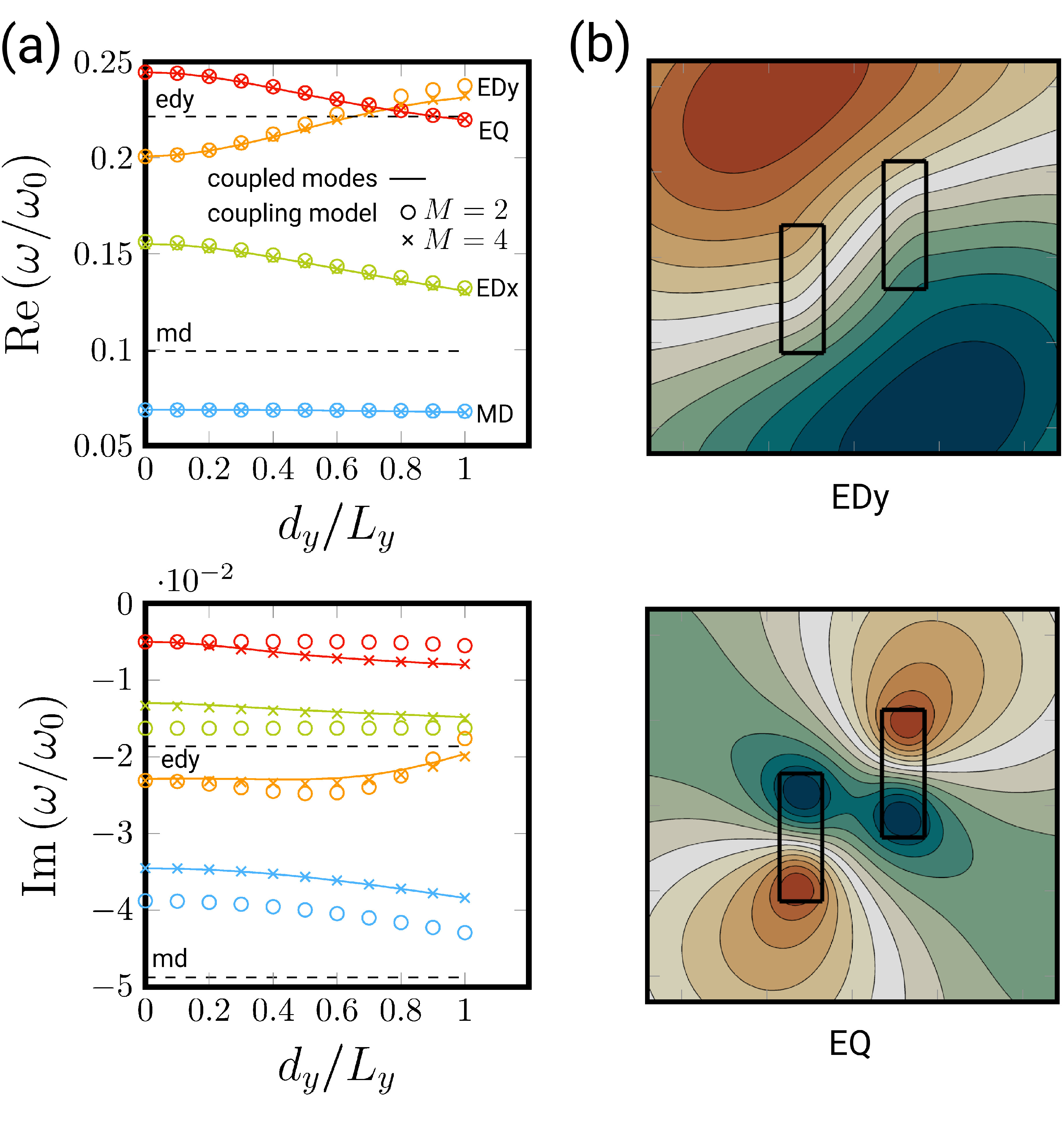
I developped a model for the coupling of quasi-normal modes in open photonic systems consisting of two resonators. By expressing the modes of the coupled system as a linear combination of the modes of the individual particles, we obtain a generalized eigenvalue prob- lem involving small size dense matrices. We apply this technique to dielectric rod dimmer of rectangular cross section for Transverse Electric (TE) polarization in a two-dimensional (2D) setup. The results of our model show excellent agreement with full-wave finite element sim- ulations. We provide a convergence analysis, and a simplified model with a few modes to study the influence of the relative position of the two resonators. This model provides interesting physical insights on the coupling scheme at stake in such systems and pave the way for systematic and efficient design and optimization of resonances in more complicated systems, for applications including sensing, antennae and spectral filtering.
