Quasi Normal Modes
Resonance is a central phenomenon in physics. In the context of electromagnetism, I study open resonators to predict their spectral properties through the computation of their quasi-normal modes associated with complex eigenfrequencies of Maxwell’s operator.
Open resonators and quasimodal expansion
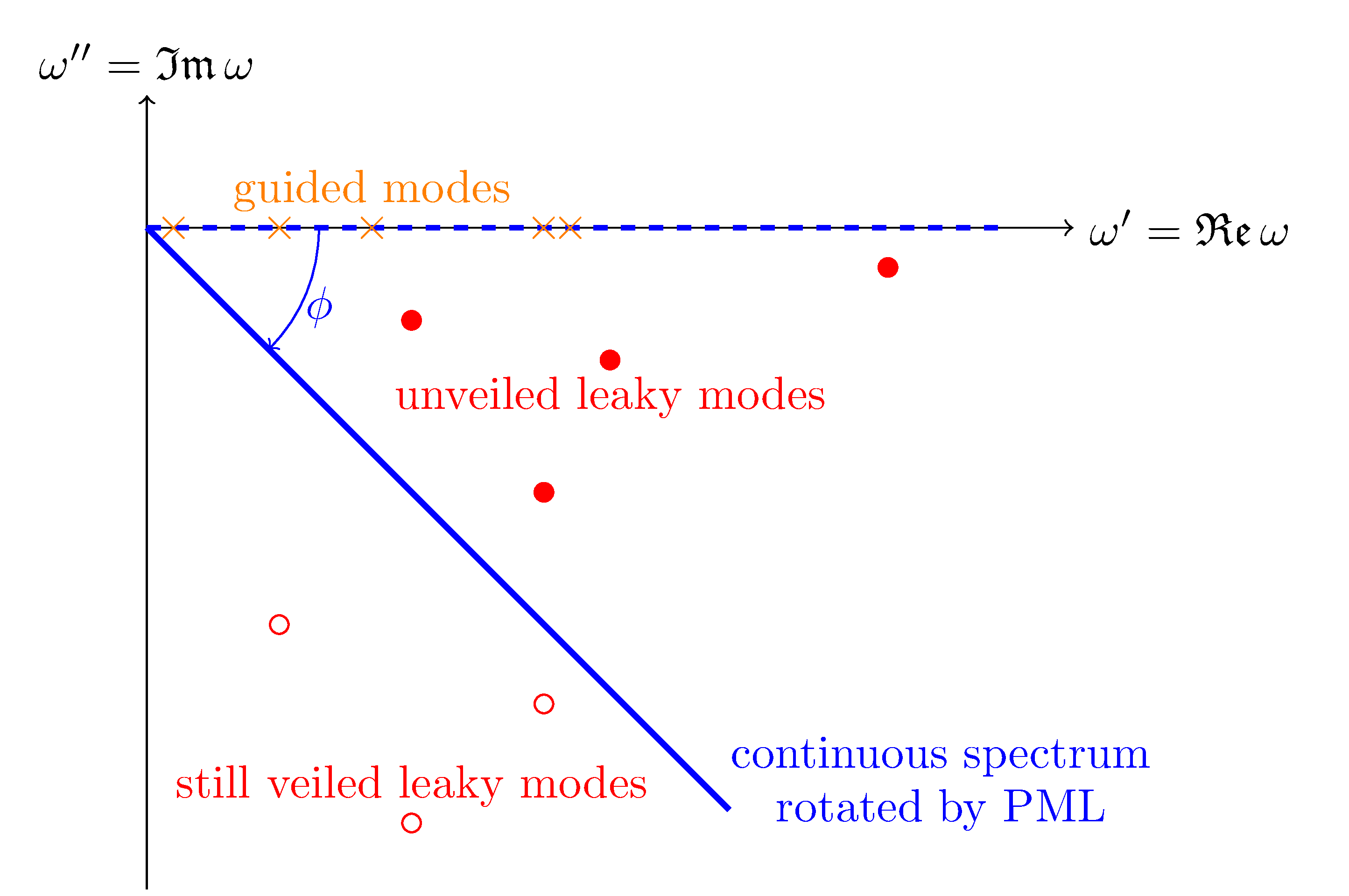
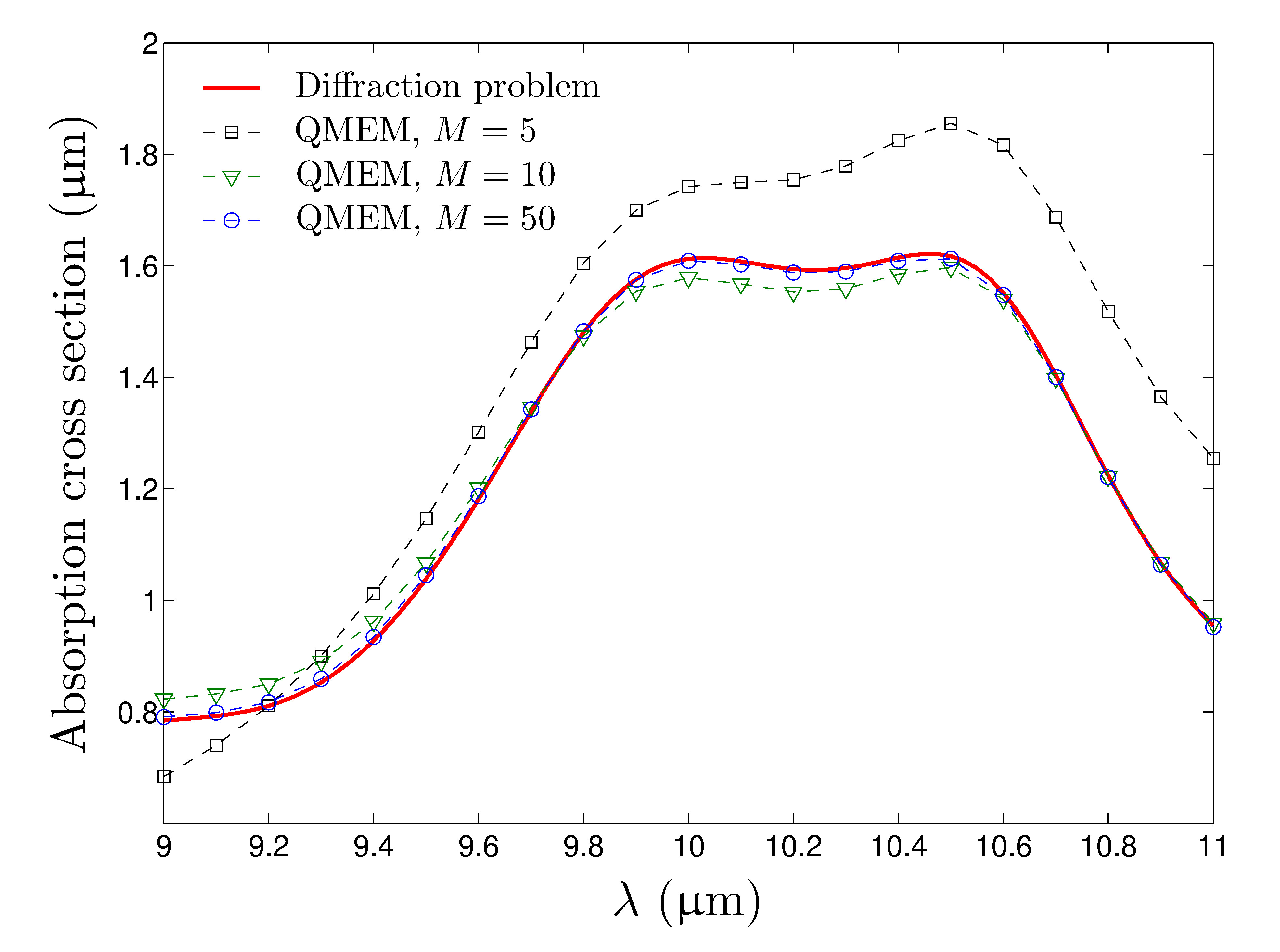
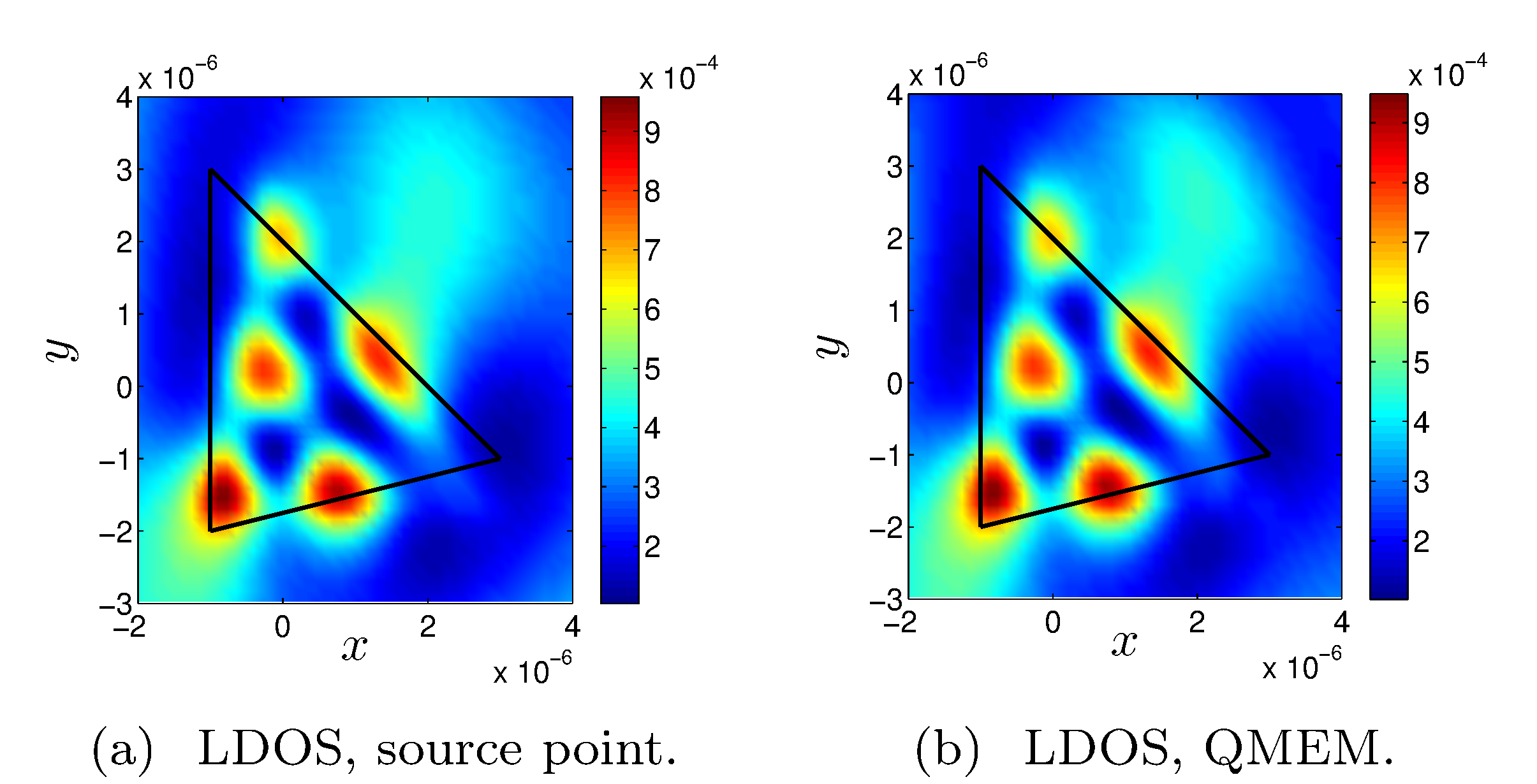
During my PhD, I developed a quasimodal expansion method (QMEM) to model and understand the scattering properties of arbitrary shaped two-dimensional open structures. In contrast with the bounded case which has only a discrete spectrum (real in the lossless media case), open resonators show a continuous spectrum composed of radiation modes and may also be characterized by resonances associated to complex eigenvalues (quasimodes). The use of a complex change of coordinates to build perfectly matched layers allows the numerical computation of those quasimodes and of approximate radiation modes. Unfortunately, the transformed operator at stake is no longer self-adjoint, and classical modal expansion fails. To cope with this issue, we consider an adjoint eigenvalue problem whose eigenvectors are biorthogonal to the eigenvectors of the initial problem. The scattered field is expanded on this complete set of modes leading to a reduced order model of the initial problem. The different contributions of the eigenmodes to the scattered field unambiguously appears through the modal coefficients, allowing us to analyze how a given mode is excited when changing incidence parameters. This gives physical insights to the spectral properties of different open structures such as nanoparticles and diffraction gratings. Moreover, the QMEM proves to be extremely efficient for the computation of local density of states.
Related article
- B. Vial, F. Zolla, A. Nicolet, and M. Commandré, Quasimodal expansion of electromagnetic fields in open two-dimensional structures. Phys. Rev. A 89 (2):023829, (2014) DOI | URL
Coupling model and mode hybridization
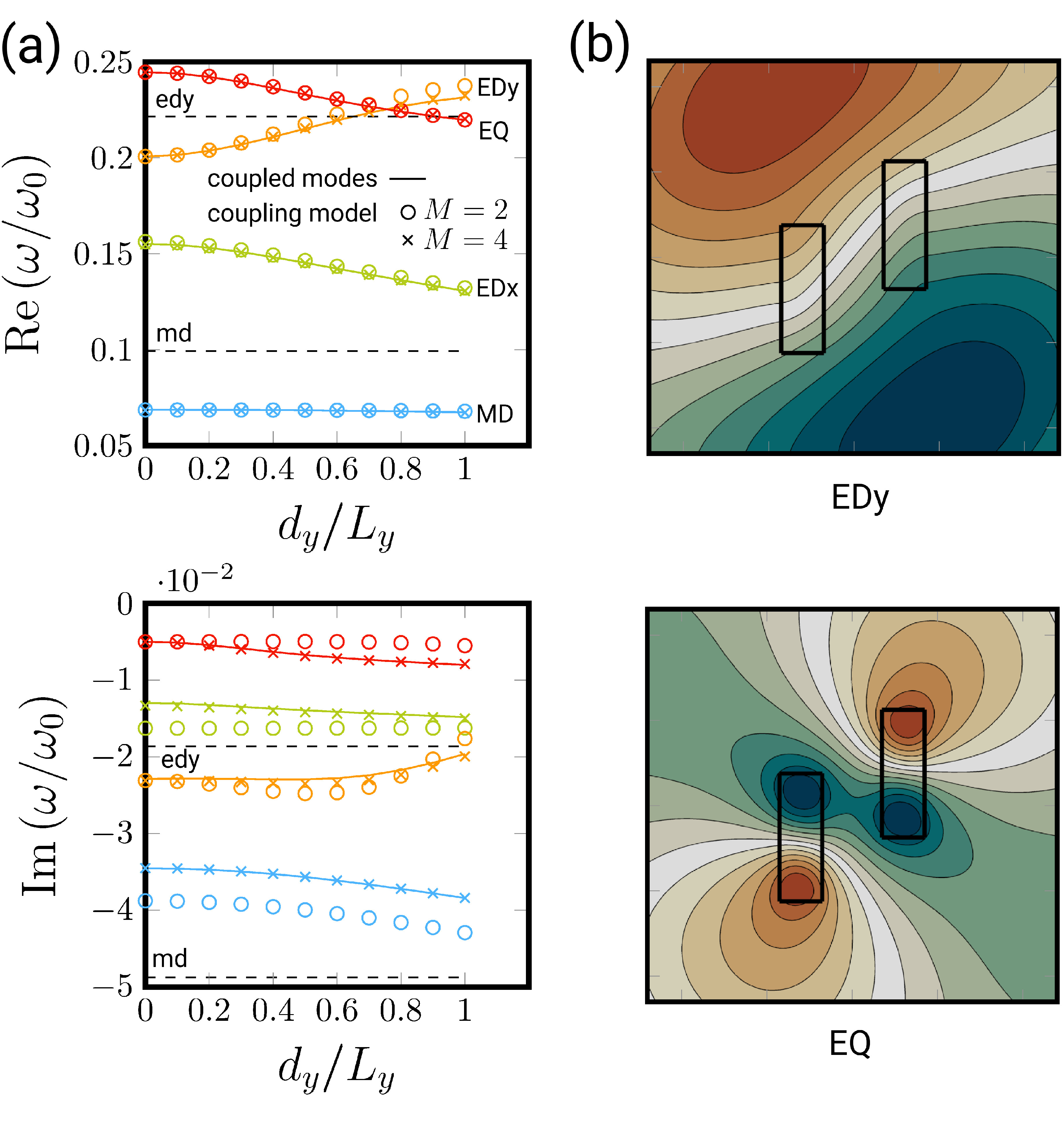
I developped a model for the coupling of quasi-normal modes in open photonic systems consisting of two resonators. By expressing the modes of the coupled system as a linear combination of the modes of the individual particles, we obtain a generalized eigenvalue prob- lem involving small size dense matrices. We apply this technique to dielectric rod dimmer of rectangular cross section for Transverse Electric (TE) polarization in a two-dimensional (2D) setup. The results of our model show excellent agreement with full-wave finite element sim- ulations. We provide a convergence analysis, and a simplified model with a few modes to study the influence of the relative position of the two resonators. This model provides interesting physical insights on the coupling scheme at stake in such systems and pave the way for systematic and efficient design and optimization of resonances in more complicated systems, for applications including sensing, antennae and spectral filtering.
Related article
Quasinormal mode expansion in thin elastic plates
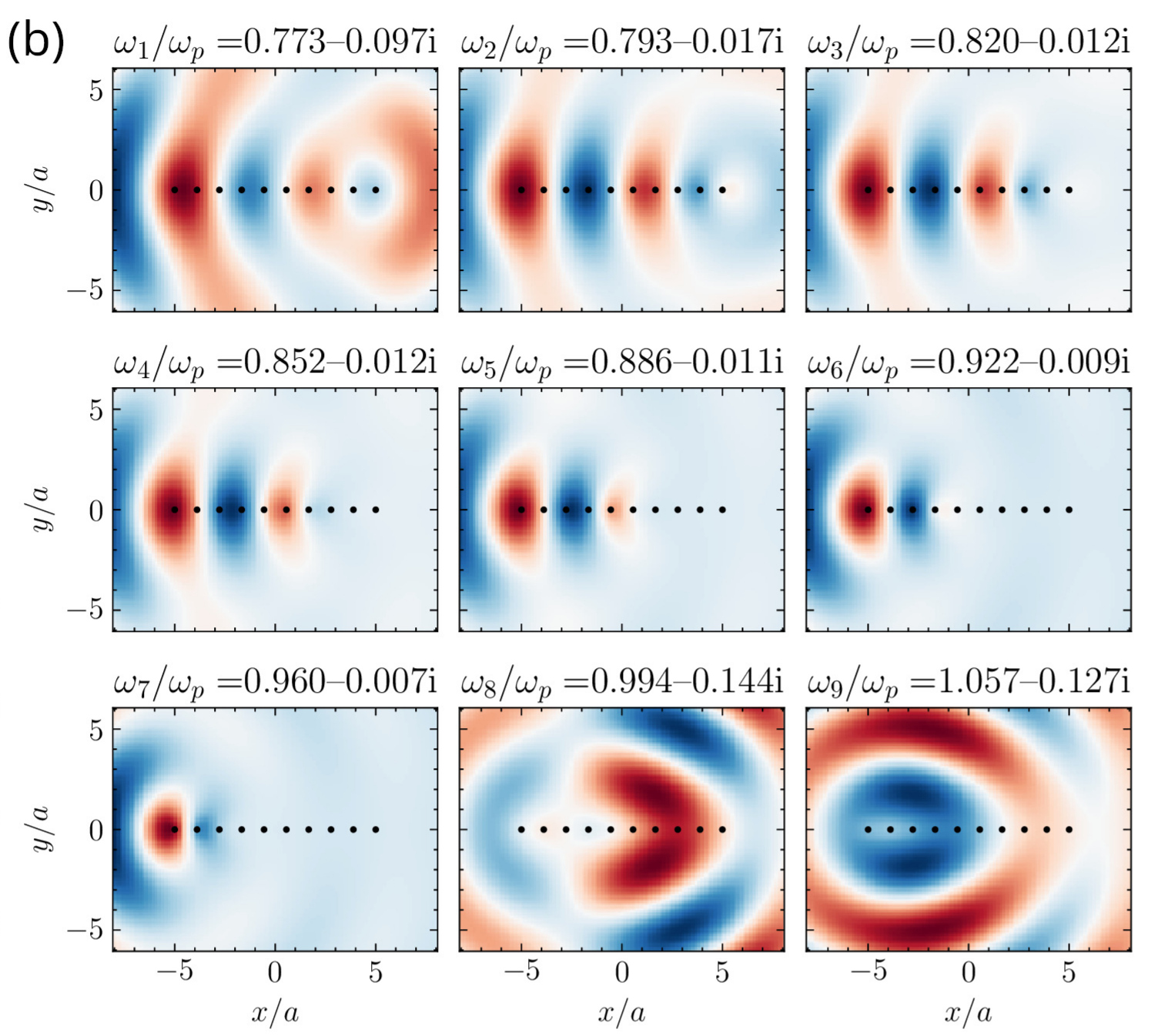
I develop a quasinormal mode (QNM) framework for the analysis and control of elastic waves in thin plates loaded with resonant scatterers. Building on the Green’s function formalism for flexural waves, the method naturally addresses multiple scattering and leads to a nonlinear eigenvalue problem whose solutions define the resonant modes of open elastic systems.
From this formulation, I derive a dispersive QNM expansion that provides a reduced-order model for efficient forced-response computations while retaining clear physical insight into resonant mode excitation. The theory also yields analytical sensitivities of the eigenfrequencies with respect to resonator parameters, enabling gradient-based optimization. This approach is used to design quasi–bound states in the continuum and to precisely position resonances in the complex frequency plane. The method is validated through scattering simulations in structured systems such as graded line arrays and elastic quasicrystals, demonstrating the power of QNM concepts for advanced elastic metamaterial design.
Related article
- B. Vial, M. Martí Sabaté, R. Wiltshaw, S. Guenneau, and R. V. Craster, Quasinormal mode expansion in thin elastic plates. Phys. Rev. B 110, 174305 (2024) DOI | URL
Related code
- B. Vial & M. Martí Sabaté, klove: Numerical modelling of waves on thin elastic plates (2024). gitlab
Quasinormal modes of Floquet media slabs
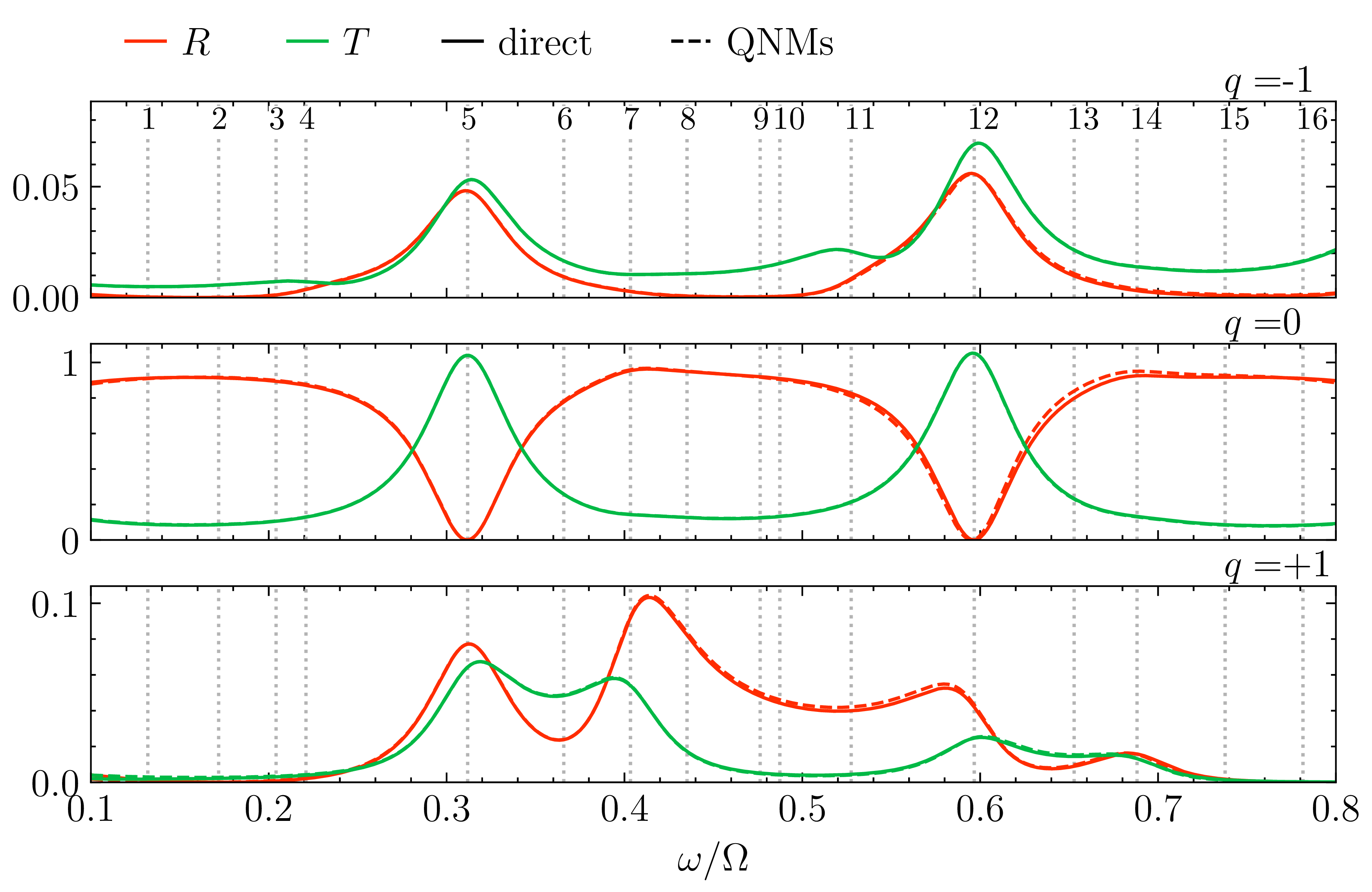
I develop a quasinormal mode (QNM) framework for the analysis of electromagnetic scattering in time-periodically modulated media. Focusing on slab geometries with temporally varying permittivity, the approach bridges concepts from photonic QNMs and Floquet theory, leading to a nonlinear eigenvalue problem that characterizes the resonant structure of open time-modulated systems.
From this formulation, I derive a QNM expansion that captures the resonant features induced by temporal modulation and provides a reduced-order model for efficient computation of scattered fields. The theory reveals how time modulation couples to resonant modes, enabling non-Hermitian gain–loss engineering and selective control of modal contributions. The framework is validated through numerical experiments on time-modulated slabs, and is used to design excitation strategies that amplify or suppress specific resonances, laying the groundwork for dynamically reconfigurable photonic devices with tailored scattering properties.
Related article
- B. Vial and R. V. Craster, Quasinormal modes of Floquet media slabs. Phys. Rev. B 112, 214201 (2025) DOI | URL
Related code
- B. Vial, pytmod: Time modulated wave solver (2025). github
